

You may have noticed that all of the equations we have solved so far have been of the form \(x+a=b\) or \(x−a=b\). We were able to isolate the variable by adding or subtracting the constant term on the side of the equation with the variable. Now we will see how to solve equations that have a variable multiplied by a constant and so will require division to isolate the variable.
Let’s look at our puzzle again with the envelopes and counters in Figure \(\PageIndex\).
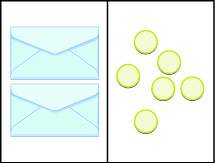
In the illustration there are two identical envelopes that contain the same number of counters. Remember, the left side of the workspace must equal the right side, but the counters on the left side are “hidden” in the envelopes. So how many counters are in each envelope?
How do we determine the number? We have to separate the counters on the right side into two groups of the same size to correspond with the two envelopes on the left side. The 6 counters divided into 2 equal groups gives 3 counters in each group (since \(6\div 2=3\)).
What equation models the situation shown in Figure \(\PageIndex\)? There are two envelopes, and each contains xx counters. Together, the two envelopes must contain a total of 6 counters.
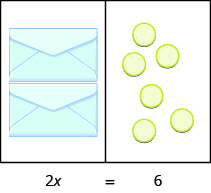
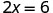 | |
| If we divide both sides of the equation by 2, as we did with the envelopes and counters, | 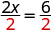 |
| we get: | 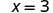 |
We found that each envelope contains 3 counters. Does this check? We know \(2\cdot 3=6\), so it works! Three counters in each of two envelopes does equal six!
This example leads to the Division Property of Equality.
For any numbers a, b, and c, and \(c\neq 0\),
When you divide both sides of an equation by any non-zero number, you still have equality.
Doing the Manipulative Mathematics activity “Division Property of Equality” will help you develop a better understanding of how to solve equations by using the Division Property of Equality.
The goal in solving an equation is to ‘undo’ the operation on the variable. In the next example, the variable is multiplied by 5, so we will divide both sides by 5 to ‘undo’ the multiplication.
Answer
| To isolate x, “undo” the multiplication by 5. | 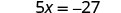 | |
| Divide to ‘undo’ the multiplication. | 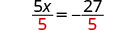 | |
| Simplify. | 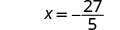 | |
| Check: | 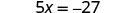 | |
| Substitute \(-\frac\) for x. | 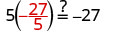 | |
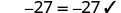 | ||
| Since this is a true statement, \(x = -\frac\) is the solution to \(5x=−27\). | ||
Answer